Lab 03: Operadores lógicos y funciones¶

Como tenemos en nuestro arsenal las estructuras de decisión, veremos otros operadores y la importancia de la programación modular (funciones). Este laboratorio tiene como propósito instruir al estudiante en los operadores de lógica presentados en clase y tambien a las funciones con su uso para reusibilidad de código. Al final del laboratorio, el estudiante tendrá una consola de Python para codificar su laboratorio. Favor de seguir las instrucciones paso por paso y favor de no saltar secciones. Recuerde que para su laboratorio, debe tener el “template” provisto por el profesor y usar comentarios en su programa.

Objetivos

En este laboratorio los estudiantes:

Aprenderán sobre operadores lógicos
Entenderán el concepto de programación modular
Aprenderán sobre funciones en Python
Apreciarán la importancia de funciones
El estudiante practicará estructuras de decisión y funciones

Operadores lógicos

Un operador lógico opera con expresiones booleanas y da como resultado cierto o falso. Los operadores más conocidos son el and, el or y not. El and y or le premite al programador conectar múltiples expresiones booleanas. El and es cierto cuando ambas subexpresiones a evaluarse son ciertas. El or es cierto cuando al menos una de las dos subexpresiones es cierta. El operador not da el resultado contrario al evaluar una expresión booleana. Como and y or operan sobre dos expresiones, se le llaman operadores binarios. A not se le llama operador unario (sobre una expresión). La importancia de estos operadores es que se pueden usar con las estructuras de decisión para verificar una expresión. Estos operadores se usan en diseño de circuitos. En Python, estos operadores pueden usarse simplemente usando las palabras and, or y not:

# Ejemplo del and
>>> x = 10
>>> st = "Odiseo"
>>> x => 5 and x < 10
False
>>> x > 9 and x == 10
True

# Ejemplo del or
>>> x > 5 or st > "Edmund"
True
>>> x > 5 or st < "Edmund"
False

# Ejemplo de not
>>> not 0
True
>>> not 5
False

Si, se pueden comparar strings! La comparación se hace a base de la tabla ascii (ver columna Decimal). Se compara letra por letra, y, en este ejemplo la letra O (79) es mayor que la letra E (45). Tambien, al negar (con el operador not) algo que no sea cero (en caso de lista, vacio), devolverá Cierto. Esto es una convención que se hace en muchos lenguajes.

Estructuras de decisión y operadores lógicos

Los operadores lógicos se usan mayormente para tomar una decisión sobre algo. Por ejemplo, imagine que quiere hacer un programa que, dado una letra verifique si es una vocal o no. Esto se puede hacer con un if y el operador lógico or. Estudie el siguiente código, donde dado una letra (se asume que el usuario va a entrar solo una letra y en minuscula), el programa imprime si es vocal o no. Utilice el espacio para practicar cualquier cosa que desee:

# Pida al usuario una letra
let = input("Ingrese una letra: ")

# Verifique condiciones
if let == "a" or let == "e" or let == "i" or let == "o" or let == "u":
    print(True)
else:
    print(False)

# Luego de correr el programa, escriba el codigo para el ejercicio
# de practica. (Borre lo anterior).

(or_y_decision)

Explicación del programa: Primero, se pide una letra al usuario. Luego se verifica si la letra insertada es una de las cinco vocales. De serlo, se imprime a la pantalla True, de lo contrario de imprime False. Note que en la linea 5 del programa se usa or para verificar si es una letra, pues queremos que sea una de ellas. Usar and para este código es erroneo, pues para ser cierto tendría que ser que una letra fuera igual a las cinco vocales, lo cual es imposible. Pregunta para usted: Si se quiere verificar que sea vocal sin importar que sea minuscula o mayuscula, ¿que cambios se le debe hacer al if*?

Ejercicio de Práctica: En el espacio anterior (luego de borrar), escriba un pedazo de código que, dado un número (float), verifique si es mayor que cero y menor o igual que 50. Esto es bueno para verificar el alcance (en ingles range) de los números en un intervalo y verificar el “input” de un usuario.

Un ejemplo algo mas largo, puede ser un programa para traducir una letra a su correspondiente traducción al alfabeto fonético NATO para telefonía. Una posible implementacion es la siguiente:

letra = input("Ingrese una letra: ")

# imprima correspodiente palabra del NATO
if letra == 'a' or letra == 'A':
    print ("Alpha")
elif letra == 'b' or letra == 'B':
    print ("Bravo")
elif letra == 'c' or letra == 'C':
    print ("Charlie")
# Siga asi hasta z:
.
.
.
elif letra == 'z' or letra == 'Z':
    print ("Zulu")
else:
    print ("letra incorrecta Insertada")

Funciones y programación modular

Digamos que usted quiere verificar si una letra es vocal, como en el ejemplo anterior. Sin embargo, ahora usted quiere verificarlo para varias letras. El problema de usar el código anterior es que usted debe repetir el código una y otra vez para verificar las letras. Por esta necesidad de reusar código, se necesitan los subprogramas, o funciones. Una función es un grupo de instrucciones que se ejecutan para llevar a cabo una tarea. Una función puede devolver un valor ( o no devolver nada). De hecho, en los laboratorios anteriores, la palabra input() en realidad es una función (al igual que print()). Las funciones tienen tres partes:

Nombre: El nombre que se le da a la función. No puede ser una palabra reservada.
Parámetros: Variables a recibirse para computar algo dentro de la función. Puede ser 0 o más parametros. Son separados por comma.
valor regresado (return type): El tipo de dato que devuelve una función. Puede ser que no devuelva nada.

Las funciones se usan para la programación modular: Dividir un programa en indepedientes subprogramas (funciones) para que cada subprograma ejecute una parte del código. Por ejemplo, si usted quiere hacer una calculadora sencilla (suma, resta, multiplicación y división), usted haría una función para cada una de las operaciones, simplificando el código.

def nombre_de_funcion(param1,param2, etc. ):
    instruccion
    instruccion
    .
    .
    return some_value

Los argumentos de una función son simplemente los valores especificos de los parametros cuando se llaman la función. Veamos como hacer una función para nuestro ejemplo:

# Definicion de una funcion. (En parentesis son los parametros)
def es_vocal(letra): # Parametro: letra
    if letra == "a" or letra == "e" or letra == "i" or letra == "o" or letra == "u":
        return True
    else:
        return False

# Llamando la funcion (usandola)
mi_letra = "u"
es_vocal("3")        # ejecuta per no se guarda su valor. Argummento: "3"
print(es_vocal("w")) # Hara print de lo que devuelva es_vocal. Argumento: "w"
ej1 = es_vocal("a")  # guardando el valor en una variable
ej2 = es_vocal("s")
ej3 = es_vocal(mi_letra)

# Haciendo prints
print(" verificando si u,a,s son vocales")
print(ej1,ej2,ej3)

(func_letra)

Note que se usa def para definir una función. El nombre de esta función es es_vocal, solo tiene un solo parámetro (letra) y regresa un booleano. Luego de definirla, se “llama” la función en el programa. Esto hace que es_vocal se ejecute y devuelva un booleano. Luego de ejecutar, el programa continua con la próxima instrucción. Importante: Todas las variables creadas dentro de una función son locales (se ven solo dentro de la función) y se eliminan cuando la función termina su ejecución.

Para ver otra utilidad de las funciones, imagine que usted quiere implementar una función que dado dos numeros, saque el cubo del número mayor. Entonces, podemos defininir una función el_mayor() para determinar el número mayor y, luego, la función cubo_del_mayor() puede usar el_mayor() dentro de su definición! Aqui la implementación, mire como la flecha roja a la izquierda se va moviendo por cada paso:

(cubo_del_mayor)

Para practicar, implemente una función el_menor() y otra cubo_del_menor() que hace lo mismo pero para el número menor. Lo importante es ver que las funciones son muy importantes a la hora de reusar código. A la vez que usted define una función, puede usarla cuantas veces sea necesario.

Tablas de Veracidad de los operadores lógicos

Para este laboratorio, implementaremos los operadores lógicos. Para esto, necesita conocer las tablas de veracidad. En otras palabras cuando es cierto y cuando es falso. En la figura siguiente, estan dichas tablas. La “n” quiere decir negación de. Por ejemplo, nand es la negación de and. La tabla de nxor es la negación de la tabla (ultima columna) de xor.

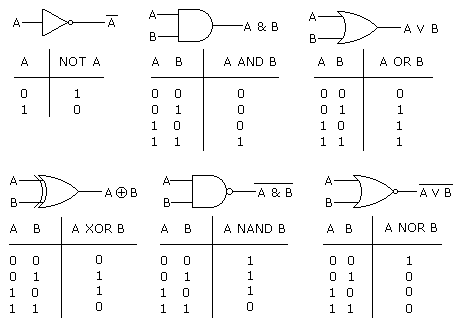
Operadores lógicos y sus tablas de veracidad

Lab: Creando los operadores lógicos¶

En este laboratorio, crearán funciones para simular los operadores lógicos que ya estan en Python y otros circuitos. Usted implementará una función por cada circuito: and, or, not, nand, nor, xor y nxor. Importante: NO puede utilizar los operadores and, or ni tampoco not de Python, solo puede usar sus funciones (dentro de otras) para que sea mas fácil crear sus funciones.

El código para el and ya esta implementado, lean el código y simplemente usen la función para construir otros operadores. Tambien, se provee el esqueleto de cada función donde usted debe llenar el código correspondiente. El último detalle es que recibirán dos parametros, ambos booleanos (excepto por not que solo recibe un booleano) y devuelve un Booleano. La palabra reservada None significa “nada”. Por ende debe cambiar esto en todas las funciones (no lo borre hasta que implemente completo su función, se usa para las pruebas que hace el código).

En el espacio provisto, se verifica si las funciones estan implementadas correctamente. Como AND esta implementado, al correr el programa saldrá cuatro veces “Pass”. Mientras siga implementando las demas funciones, pasará mas pruebas. Cuando diga “Pass” para todas las pruebas, habrá completado el laboratorio.

En especifico, para el laboratorio:

Creará una función, por cada circuito: and, or, not, nand, nor, xor y nxor (programación modular).

Todas las funciones reciben dos parametros (solo not recibe un solo parametro). Cada parametro es un booleano (True o False). (Mire la función AND dada). NO PUEDE USAR el and, or, not que provee Python para ninguna función.

Todos los nombres de las funciones tienen que ser con mayúscula (AND, OR, NOT, etc...).

Se recomienda que use las funciones que cree para usarlas en otras funciones cuando vea la oportunidad. Por ejemplo, ya que se le provee AND, implemente NOT. Luego, usando estas dos funciones puede implementar NAND. Cuando construya OR, use NOT para obtener NOR.

El NAND es un circuito universal, esto quiere decir que con NAND se puede construir los otros circuitos. Utilice esta idea para OR. Tambien puede implementarlo de una manera similar al AND dado.

Piense como puede implementar XOR en terminos de otras funciones. Tambien puede implementarlo de una manera similar al AND dado.

Para tener todo correcto, debe pasar todas las pruebas.

Utilice el siguiente espacio para codificar su laboratorio (se verifican si las funciones estan bien):

# operador AND.
# ej. a = True, b = False devolvera falso
def AND (a,b):
    if a:               # es lo mismo que a == True
        if b:           # Nested if: Si a es cierto y b es cierto
            return True # Regresa Cierto
        else:
            return False# Solo a es cierto, regresa Falso
    else:
        return False    # a no es cierto, no importa si
                        # b es cierto, regresa falso.


# Implemente los siguientes circuitos
# escriba el codigo para cada funcion (identado!)
def NOT(a):
    return None

def NAND(a,b):
    return None

def OR(a,b):
    return None

def NOR(a,b):
    return None

def XOR(a,b):
    return None

def NXOR(a,b):
    return None

(units1)

import unittestgui

class myTests(unittestgui.unittest):
    # Cannot use assertFalse() is broken
    def testAND(self): #AND
        self.assertTrue(AND(True,True),"NAND() fallo con argumentos True, True")
        self.assertEqual(AND(True,False),False,"AND() fallo con argumentos True, False")
        self.assertEqual(AND(False,True),False,"AND() fallo con argumentos False, True")
        self.assertEqual(AND(False,False),False,"AND() fallo con argumentos False, False")

    def testNOT(self): #NOT
        self.assertEqual(NOT(True),False,"NOT() fallo con argumento True")
        self.assertTrue(NOT(False),"NOT() fallo con argumento False")

    def testNAND(self): #NAND
        self.assertEqual(NAND(True,True),False,"NAND() fallo con argumentos True, True")
        self.assertTrue(NAND(True,False),"NAND() fallo con argumentos True, False")
        self.assertTrue(NAND(False,True),"NAND() fallo con argumentos False, True")
        self.assertTrue(NAND(False,False),"NAND() fallo con argumentos False, False")

    def testOR(self): #OR
        self.assertTrue(OR(True,True),"OR() fallo con argumentos True, True")
        self.assertTrue(OR(True,False),"OR() fallo con argumentos True, False")
        self.assertTrue(OR(False,True),"OR() fallo con argumentos False, True")
        self.assertEqual(OR(False,False),False,"OR() fallo con argumentos False, False")

    def testNOR(self): #NOR
        self.assertEqual(NOR(True,True),False,"NOR() fallo con argumentos True, True")
        self.assertEqual(NOR(True,False),False,"NOR() fallo con argumentos True, False")
        self.assertEqual(NOR(False,True),False,"NOR() fallo con argumentos False, True")
        self.assertTrue(NOR(False,False),"NOR() fallo con argumentos False, False")

    def testXOR(self): #XOR
        self.assertEqual(XOR(True,True),False,"XOR() fallo con argumentos True, True")
        self.assertTrue(XOR(True,False),"XOR() fallo con argumentos True, False")
        self.assertTrue(XOR(False,True),"XOR() fallo con argumentos False, True")
        self.assertEqual(XOR(False,False),False,"XOR() fallo con argumentos False, False")

    def testNXOR(self): #NXOR
        self.assertTrue(NXOR(True,True),"NXOR() fallo con argumentos True, True")
        self.assertEqual(NXOR(True,False),False,"NXOR() fallo con argumentos True, False")
        self.assertEqual(NXOR(False,True),False,"NXOR() fallo con argumentos False, True")
        self.assertTrue(NXOR(False,False),"NXOR() fallo con argumentos False, False")

myTests().main()

Nota: Si borra la definición de las funciones dadas, la consola dará un “Type Error” porque no tiene como verificar las pruebas de las funciones.

Para Entregar: Luego de terminar su laboratorio, haga “copy/paste” de su código en un file. Incluya el template como el profesor discutió en clase. Guarde el file con el nombre lab3.py. Ingrese a la clase registrada en moodle y haga “upload” de su file en el tab correspondiente. Luego de entregar el lab, favor de llenar este cuestionario. De surgir alguna duda con respecto al lab, puede enviar preguntas a Piazza.

Fecha de Entrega: Viernes 20 de marzo del 2015, antes de las 11:55pm en moodle.

Científico del día: Von Neummann. Matemático húngaro-estadounidense que hizo contribuciones en muchas ramas ( teoría de conjuntos, teoría de juegos, ciencias de la computación, economía, etc.). Inventó el concepto de ariqutectura de Von Neumann, la cual es usada actualmente en las computadoras - Un CPU con un ALU y un Control, Memoria Principal, y sistemas de entrada y salida. Se le atribuye la invención del algoritmo Merge Sort. Es considerado como uno de los más importantes matemáticos de la historia moderna. Puede leer más en Wikipedia.